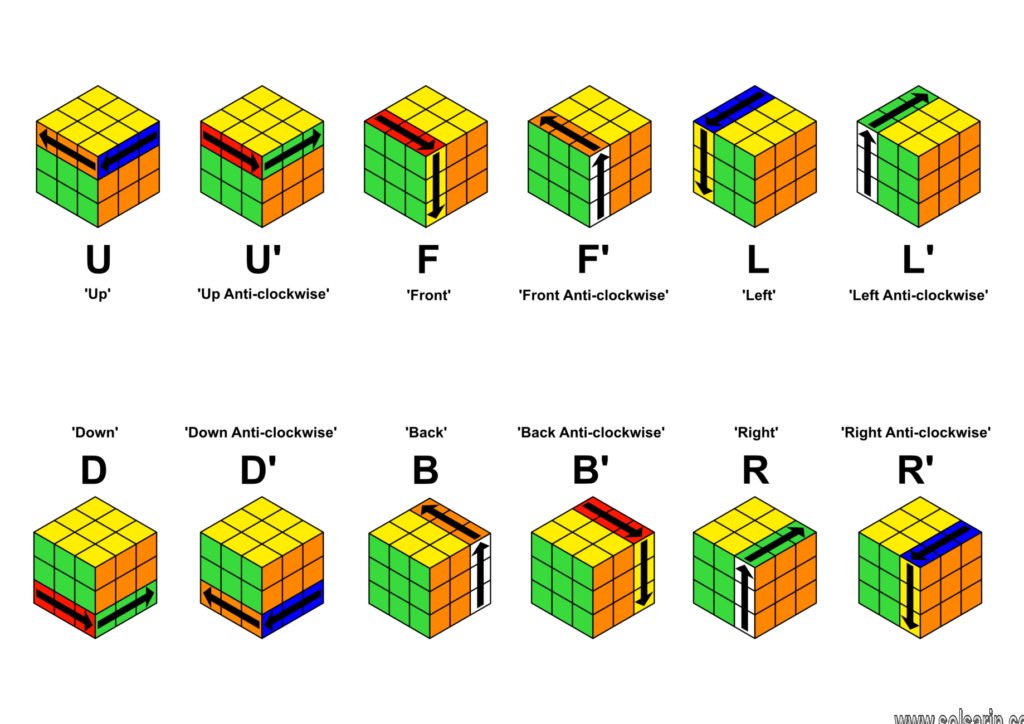
how to solve a rubik’s cube 4×4
Hello to you who are reading this post “how to solve a rubik’s cube 4×4“. Welcome to solsarin.
The Rubik’s 4×4 cube is also sometimes known as The Rubik’s Revenge. Unlike the original 3×3 cube, the 4x4x has no fixed centre pieces and so it is even harder to solve!! But don’t worry, here are some videos to help you master this difficult puzzle.
The Rubik’s Revenge (also known as the Master Cube) is a 4×4×4 version of Rubik’s Cube. It was released in 1981. Invented by Péter Sebestény, the Rubik’s Revenge was nearly called the Sebestény Cube until a somewhat last-minute decision changed the puzzle’s name to attract fans of the original Rubik’s Cube. Unlike the original puzzle (and other odd-numbered puzzles like the 5×5×5 cube), it has no fixed facets: the centre facets (four per face) are free to move to different positions.

Methods for solving the 3×3×3 cube work for ttwohe edges and corners of the 4×4×4 cube, as long as one has correctly identified the relative positions of the colours—since the centre facets can no longer be used for identification.
Solving the 4×4 Rubik’s Cube is not too much harder than solving a 3×3. The concepts of the steps are as follows:
- Solve the center pieces
- Pair similar edge pieces
- Turn only the outer layers, and solve it like a 3×3!
In this video I teach the Yau Method, which roughly follows this outline. The Yau method is the most popular 4×4 method and was used to set the current world record.
Example Solve
Here is a full solve where I go through some more possibilities of what can happen.
Step 1. White Center
Pair up 2 white center pieces to form a bar.
Make another white center bar somewhere else on the cube, and then join the 2 bars together.
This step should be completely intuitive, although you may need to experiment a bit to get used to how pieces move.
Hold the white center on the bottom, and make a yellow center bar anywhere on the cube.
Make sure to fix the white center if you ever destroy it. Examples:
If the yellow bar is not on the top face, move it onto the top by doing this:
Make another yellow bar, and then place it under the first bar to move it to the top:
The tutorial video and example solve videos above show some trickier cases for this step.
Step 3. Partial White Cross
This step completes 3 out of the 4 cross pieces in the correct color order.
Hold the white center on the left.
The correct color order going upwards is Blue, Orange, Green, Red (BOGR)
Example of a finished cross and centers:
Find 2 white edge pieces that have the same colors on them.
Put one in the left slice layer, and one in the right slice layer (the slice layers are the middle 2 layers).
Join them, and add it to the cross.
Repeat this step for a total of 3 (not 4) cross pieces solved, and follow the color scheme shown above.
Be careful not to destroy other cross pieces or the 2 solved centers.


Step 4. Centers
Make 1 center bar of any color, and turn it to be vertical.
Be careful not to destroy the partial cross (tips explained in the video tutorial).
If you have completed any other centers already, make sure you also fix them any time you break them (just like fixing the white center when making the yellow center).
Make another center bar of the same color.
If this is the first center you’ve made, you can just join them together.
If other centers have already been made, put the 2 bars on the same side to join them:
Solve the rest of the centers.
Some trickier cases for the last 2 centers are shown in the example solve video above.
Step 5. Edge Pairing
Hold the cross on the bottom, with the unsolved part at the front.
Look for the last 2 white edge pieces. If one is in the bottom, turn the front so that it’s not.
Put both white pieces in the front/left and front/right without breaking the partial cross.
Each piece is either on the top or bottom slice layer.
Case 1: If they are in different slices:
- Join the pieces
- Replace it with an unsolved edge pair
- Fix the centers
Note: the edge pair coming down must be an unsolved pair.
Case 2: If they are in the same slice:
- Slice piece 1 towards piece 2.
- Flip piece 1 (with the flipping algorithm: R U R’ F R’ F’ R)
- Fix the centers
Insert the cross edge into the bottom layer to complete the cross.
Solve the rest of the edge pairs one at a time using the same method as for the first edge. If you are ever confused, you can watch the example solve video above as it shows the full process.


Step 6. Solve Like a 3×3! (mostly)
Step 7: Parity cases
As you reach the last layer you might find yourself in a situation where the cube seems to be unsolvable. For example when you reach the yellow cross and one edge seems to be oriented wrong or you find two pieces on the correct spot when you are positioning the last layer corners. See which of the long algorithms below solves your situation.
What is OLL parity?
OLL parity is when only one edge block is not oriented. This is an impossible case in a regular 3×3 cube. This case is solved using the algorithm above. It’s important to execute the OLL parity algorithm, if needed, before solving the last layer, because it does not preserve the last layer pieces positions. The probability to encounter an OLL parity during a 4×4 solve is 50%
What is PLL parity?
PLL parity is when only 2 edge pieces are remained unsolved while the rest of the cube is fully solved. This case also cannot happen on a 3×3 cube (reasons below), and is being fixed by the PLL parity algorithm. The PLL parity algorithm does preserve all pieces but the switched edge pieces, and therefore can be used at the end of the solving (after solving all other last layer pieces). The probability to encounter a PLL parity during a 4×4 solve is 50%
Note! You might encounter a weird PLL case, where all pieces are solved but 2 corners for example. That’s because of the PLL parity. After applying the PLL parity algorithm it’ll become a solvable PLL case.
Notations explanation: The PLL parity uses an internal layer movement. The number “2” shown before the specified face letter, means moving the internal layer of its face. Example: [2R] = [r R’]. The move “2R” can be done by moving both layers by doing r, and then returning the R face back by doing R’. The move “2R2” means moving this internal layer twice. You can see image examples in the intro section above.
Why PLL parity occurs on 4×4 cubes while it’s impossible on a regular 3×3 cube?
The reason is because of the mechanics and math of the Rubik’s cube. As you know, moving only 2 edge pieces while preserving all other pieces is impossible* (U-perm algorithm affects 3 edge pieces, which is the lowest possible). Moving only one piece is clearly impossible (where will it go without switching with another piece?).
Therefore, a case where only 2 edge pieces needed to be switched is an impossible case on a 3×3 cube. However, on a 4×4 cube it’s not really 2 pieces, but 4 pieces, and 4 pieces needed to be switched between is a possible case.
What about OLL parities?
OLL parity happens in the 4×4 cube for the same reasons as well. The minimum number of pieces orientation while preserving all other pieces is 2 (applies for all sizes of cubes). Therefore it’s impossible that only 1 edge piece will be un-oriented in a 3×3 cube. While in a 4×4 cube it is actually 2 different edge pieces (even though we treat them as “one edge block”) which is a possible case.
After understanding the parities, let’s continue and finish solving the 4×4 cube:
If after completing step 3 (solving the cube until the last layer) you noticed that an OLL parity occur- then apply the algorithm and continue in solving the last layer using the 3×3 solving technique. Apply a PLL algorithm as well if needed.
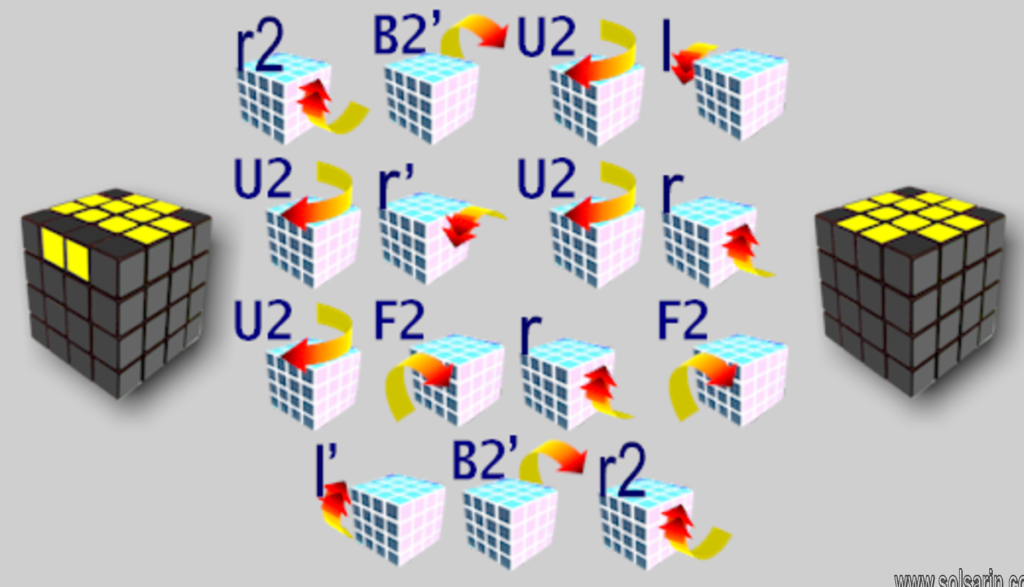

Parity errors
Certain positions that cannot be solved on a standard 3×3×3 cube may be reached. There are two possible problems not found on the 3×3×3. The first is two edge pieces reversed on one edge, resulting in the colours of that edge not matching the rest of the cubies on either face (OLL parity):
Notice that these two edge pieces are swapped. The second is two edge pairs being swapped with each other (PLL parity), may be two corners swapped instead depending on situation and/or method:
Some methods are designed to avoid the parity errors described above. For instance, solving the corners and edges first and the centres last would avoid such parity errors. Once the rest of the cube is solved, any permutation of the centre pieces can be solved. Note that it is possible to apparently exchange a pair of face centres by cycling 3 face centres, two of which are visually identical.These situations are known as parity errors. These positions are still solvable; however, special algorithms must be applied to fix the errors.
PLL parity occurs on all cubes with an even number of edges from the 4x4x4 onwards. It does not, however, occur on cubes with an odd number of edges, such as the 3x3x3 and the 5x5x5. This is due to the fact that the latter have fixed center pieces and the former do not.
Direct solving of a 4×4×4 is uncommon, but possible, with methods such as K4. Doing so mixes a variety of techniques and is heavily reliant on commutators for the final steps.
That’s it! You had just solved the 4×4 Rubik’s Revenge! Just keep and practice on solving the 4×4 cube till you‘ll be able to do it without using this guide. You will be happy to know that you have to memorize only 4 algorithms for that (2 parities + 2 algorithms from step 2)! Congratulations!
Thanks for taking the time to read this post “how to solve a rubik’s cube 4×4”.




