symmetric property of congruence

symmetric property of congruence

Hello dear friends, thank you for choosing us. In this post on the solsarin site, we will talk about “symmetric property of congruence”.
Stay with us.
Thank you for your choice.

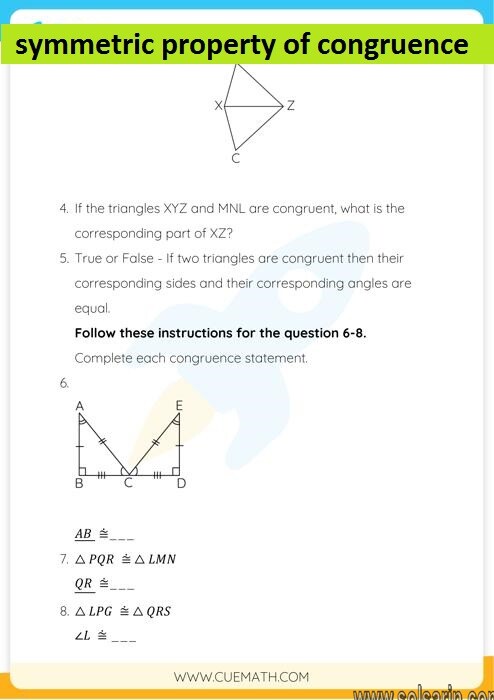
symmetric property of congruence

Transitive Property of Congruence

Congruence is a term used to describe when two shapes or figures have the same shape and size. Transitive property of congruence means.

if one pair of lines or angles or triangles are congruent to a third line or angle or triangle.

then the first line or angle or triangle is congruent to the third line or angle or triangle.

As mentioned, the transitive property establishes an equivalence relation between 3 lines, 3 angles and 3 triangles.

The definition of the transitive property of congruence in geometry states that if any two angles, lines, or shapes are congruent to a third angle, line, or shape respectively.

then the first two angles, lines, or shapes are also congruent to the third angle, line, or shape. For example, if ∠A is congruent to angle B.

and angle B is congruent to angle C, then as per the transitive property of congruence, angle A is congruent to angle C.

Two triangles are said to be congruent if they have the same shape and size. Also, the two triangles have the same side length and angles.

If one triangle is flipped, rotated or transformed to get the exact shape and size of the second triangle.

and it still does not undergo any transformation in its shape, size, angles or any other dimensions, then we can say that the first triangle is congruent to the second triangle.

Sometimes, the term ”Similar triangles’ is confused with ‘Conguent triangles’. The difference between them is that, two triangles are said to be similar.

if they have the same shape, but are different in size, whereas two triangles are said to be congruent, if their shapes and size exactly match with each other.

The transitive property of congruence is only applicable if there are more than 2 angles. line segments or shapes. The figure given below, shows two congruent triangles.

The curved and straight line markings denote that the corresponding sides and angles are equal.

Properties of Congruence

There are three properties of congruence. They are reflexive property, symmetric property and transitive property.

All the three properties are applicable to lines, angles and shapes.

• Reflexive property of congruence means a line segment, or angle or a shape is congruent to itself at all times.
• Symmetric property of congruence means if  shape 1 is congruent to shape 2, then we can say that shape 2 is also congruent to shape 1.

Transitive property of congruence involves 3 lines or angles or shapes. It states that if shape 1 is congruent to shape 2 and shape 2 is also congruent to shape 3, then we can say that shape 1 is congruent to shape 3.

There are certain criteria to refer two triangles to be congruent.

They are SSS criterion, SAS criterion, ASA criterion, AAS criterion, and HL criterion. Let us look at each of them in detail.

SSS Criterion

SSS is the short form of Side-Side-Side. When the sides of two triangles are the same, they are said to be congruent by SSS criterion.

Here in the figure given below, triangle ABC is congruent to triangle XYZ by SSS criterion.

 

ASA Criterion

ASA Criterion stands for Angle-Side-Angle Criterion. Under this criterion, if the two angles and the side included between them of one triangle are equal to the two corresponding angles.

and the side included between them of another triangle, the two triangles are congruent.

SAS Criterion

SAS is the short form of Side-Angle-Side. When two sides and the included angle of a triangle is equal to the the two sides and the included angle of another triangle.

then these two traingles are said to be congruent by SAS criterion. In the figure shown below triangle ABC is congruent to triangle XYZ by SAS criterion.

ASA Criterion

ASA Criterion stands for Angle-Side-Angle Criterion. Under this criterion, if the two angles and the side included between them of one triangle are equal to the two corresponding angles and the side included between them of another triangle, the two triangles are congruent.

AAS criterion

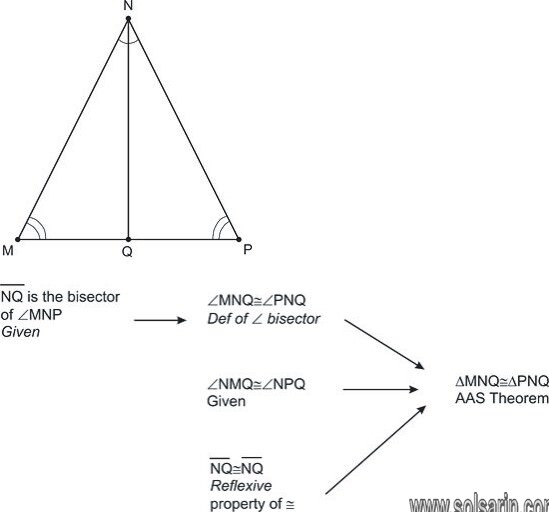
AAS Criterion stands for Angle-Angle-Side Criterion. It states that, if the two angles and the non-included side of one triangle are equal to the two corresponding angles and the non-included side of another triangle, the triangles are congruent.

HL Criterion

HL Criterion stands for Hypotenuse-Leg Criterion. Under this criterion, if the hypotenuse and side of one right-angled triangle are equal to the hypotenuse and the corresponding side of another right-angled triangle, the two triangles are congruent.

Let’s say we have 3 triangles △ABC, △DEF, and △PQR. As △ABC and △DEF are same in shape and size, △ABC ≅ △DEF. Similarly, as △DEF and △PQR are same in shape and size.

△DEF ≅ △PQR. Thus, as per the transitive property of congruent triangles, △ABC ≅ △PQR. The three triangles are said to be similar.

which means they are of the same shape and congruent as well. If the triangles are only similar, we can say that all the corresponding interior angles are equal, but they differ in their side length.

Let’s take a look at transitive property of congruence examples.

Transitive Property of Congruence for Angles

For angles m, n, and p, if ∠m ≅ ∠n and ∠n ≅ ∠p, then by transitive property of congruent angles, ∠m ≅ ∠p. When two angles are congruent to a third angle, then all the angles are congruent to each other.

Are parallel lines Congruent?

Let’s say we have 3 parallel lines.

As the figure shows, line a ∥ line b. And, line b ∥ line c. Hence, by transitive property of congruence for parallel lines, line a ∥ line c.

Topics Related to Transitive Property of Congruence

Important Notes

Transitive property of congruence applies to 3 figures.

Transitive property of congruence is applicable to lines, angles and shapes.

According to the transitive property of congruence of triangles, 3 triangles are equal in shape, size and measure of angles and sides.