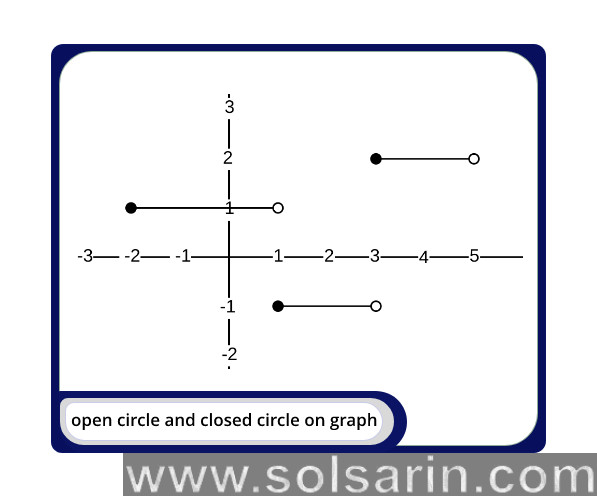
open circle and closed circle on graph
Welcome to Solsarin. In this article we want to talk about graph open circle closed circle.
Can you explain the difference between an open and closed circle?
The answer to this question needs to be explained with a diagram!
Count all the real numbers between 2 and 4, excluding 4 but including 2.
As a result, we would write this as… 2 ≤ x < 4
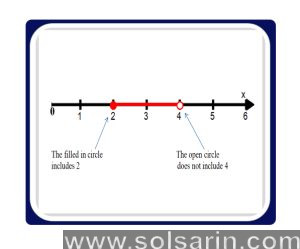

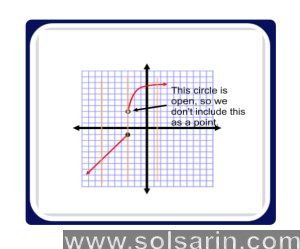
graph open circle closed circle
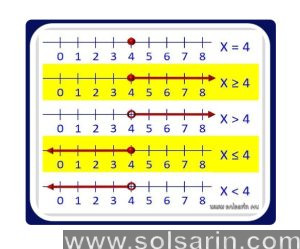
An inequality greater than ( ) or less than ( ) is represented with a closed, or shaded, circle. Solution includes the point. There are two types of open circles: ones that go over (>) and those that go under (<).
Numerical inequalities
Numbers that are not equal to each other are called inequalities. The inequality sign will be used when there is an inequality:
< less than
≤ less than or equal to;
> greater than;
≥ greater than or equal to.
When it comes to algebra, an inequality is defined as a number or range of numbers that are either greater than, greater than or equal to, less than, or less than or equal to a fixed value.
Number lines and circles can be used to illustrate this. Lines indicate possible values. It is the circle that marks the end of the line.
In the case of a filled circle, the value is equal to or greater/less than the fixed value. A circle with an empty center does not include the fixed value.
the circle is not filled so the value is less than
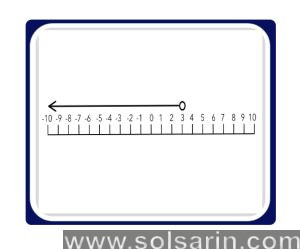

Since the circle is filled, the value is less than or equal to


-3 is not included (unfilled). There is a 5 included (filled)
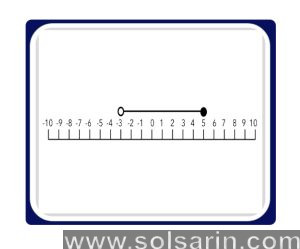

When a dot is open, does it mean it’s equal?
A solid dot on a number line graph indicates that the given number could be a possible solution, whereas an open dot indicates the number cannot be a solution. You would place an open dot at 7 if the graph x > 7 is invalid (7 cannot be greater than itself).
When a circle is closed, does it mean it has been included?
The circle indicates whether or not a number is included on a number line when we graph inequalities. When a circle is open, it indicates that the number is not included, while when it is closed, it includes the number. We use square brackets and parenthesis when writing inequalities using interval notation.
An inequality is graphed with a closed circle. What does that mean?
Inequality Graph Tutorial-Example Question #1 Explanation: Closed circles indicate “greater than” or “less than,” while open circles indicate “greater than” or “less than.”.
In a number line, what does it mean when a circle is closed or open?
Numbers are represented by open circles when they are smaller or larger than the indicated value (< or >). Those circles that are closed are considered numbers that are less than or equal to or greater than or equal to the specified number (≤ or ≥).
When it comes to limits, what does a closed circle mean?
The reason for the existence of the limit is the fact that the same y-value is approached from both sides. Since the open circle in the graph is simply a gap, the graph does not have two places where it can be found. If x = 7 then the closed circle represents the actual value of the y-axis at y=7 as well.
In an open circle, is it possible to have a limit?
Open circles (also called removable discontinuities) are holes in a function – one particular value of x without a value of f(x). There still exists a limit if a function approaches the same value from both the positive and negative sides.

Can a hole be filled to a certain limit?
If the graph is hollow at the point where x is approaching, with no other points for other values of the function, then the limit still exists.
In what circumstances does there not exist a limit?
Graphs and Limits
- At the point x = c, if there is a gap in the graph, the two-sided limit will not exist.
- A graph with a vertical asymptote that goes towards infinity on one side and negative infinity on the other does not have a limit.
In the event that a limit equals 0, what happens?
There is no limit, so there is no limit. In this case, the denominator increases faster than the numerator, so the fraction tends to zero as the denominator decreases. For example, if g(x), the denominator, has a higher power than f(x), the numerator.
In the case of a zero numerator, what happens?
There is no problem with a fraction’s numerator taking on the value of zero. Legal fractions (denominators other than zero) with numerators equal to zero have a value of zero overall. Numerators equal zero, so all fractions have zero value.
Negative numerators are possible?
It is common to see a fraction with a negative denominator or numerator, but not always. A fraction with a negative numerator and denominator is positive because a negative is divided by a negative.
What are the chances that a fraction can be zero?
There are no shaded parts in the fractional notation of Zero, thus this form can be written in fractional form as . It is true that if we divide an object into n parts and take none of them, we get the value 0.
Can you tell me what the slope of the denominator is when the denominator is 0?
It should be noted that if the denominator of the fraction is 0 then the slope will be undefined. This occurs when both points are on the same side of the line, with the same value of x. A vertical line would be drawn on the graph to show that the value of x will remain constant regardless of what value of y is chosen.
In what ways does a slope differ from another type of slope?
An undefined slope, or an infinite slope, can be defined as a line that neither moves left nor right, as opposed to a vertical line, which moves up and down.
last word
I hope this article answers your questions and be useful.
read more:
- is alice in wonderland public domain
- how many players on baseball team
- fastest dog in the world
- how do i find my naics number
- 1969 “volkswagen beach bomb” prototype
- what did transcendentalists believe?
- john mccain mother age
- when did star wars action figures come out?
- healthy dinner ideas vegetarian