prime factorization of 16
Hello. Welcome to solsarin. This post is about “prime factorization of 16“.
Mathematics
Mathematics (from Ancient Greek μάθημα (máthēma) ‘knowledge, study, learning’) is an area of knowledge, which includes the study of such topics as numbers (arithmetic and number theory),[1] formulas and related structures (algebra),[2] shapes and spaces in which they are contained (geometry),[1] and quantities and their changes (calculus and analysis).[3][4][5] There is no general consensus about its exact scope or epistemological status.[6][7]
Most of mathematical activity consists of discovering and proving (by pure reasoning) properties of abstract objects. These objects are either abstractions from nature (such as natural numbers or lines), or (in modern mathematics) abstract entities of which certain properties, called axioms, are stipulated. A proof consists of a succession of applications of some deductive rules to already known results, including previously proved theorems, axioms and (in case of abstraction from nature) some basic properties that are considered as true starting points of the theory under consideration. The result of a proof is called a theorem.
Newton’s law
Mathematics is widely used in science for modeling phenomena. This enables the extraction of quantitative predictions from experimental laws. For example, the movement of planets can be predicted with high accuracy using Newton’s law of gravitation combined with mathematical computation. The independence of mathematical truth from any experimentation implies that the accuracy of such predictions depends only on the adequacy of the model for describing the reality.


Integer factorization
In number theory, integer factorization is the decomposition of a composite number into a product of smaller integers. If these factors are further restricted to prime numbers, the process is called prime factorization.
When the numbers are sufficiently large, no efficient, non-quantum integer factorization algorithm is known. However, it has not been proven that no efficient algorithm exists. The presumed difficulty of this problem is at the heart of widely used algorithms in cryptography such as RSA. Many areas of mathematics and computer science have been brought to bear on the problem, including elliptic curves, algebraic number theory, and quantum computing.
In 2019, Fabrice Boudot, Pierrick Gaudry, Aurore Guillevic, Nadia Heninger, Emmanuel Thomé and Paul Zimmermann factored a 240-digit (795-bit) number (RSA-240) utilizing approximately 900 core-years of computing power.[1] The researchers estimated that a 1024-bit RSA modulus would take about 500 times as long.[2]
Fermat’s factorization method
Not all numbers of a given length are equally hard to factor. The hardest instances of these problems (for currently known techniques) are semiprimes, the product of two prime numbers. When they are both large, for instance more than two thousand bits long, randomly chosen, and about the same size (but not too close, for example, to avoid efficient factorization by Fermat’s factorization method), even the fastest prime factorization algorithms on the fastest computers can take enough time to make the search impractical; that is, as the number of digits of the primes being factored increases, the number of operations required to perform the factorization on any computer increases drastically.
Many cryptographic protocols are based on the difficulty of factoring large composite integers or a related problem—for example, the RSA problem. An algorithm that efficiently factors an arbitrary integer would render RSA-based public-key cryptography insecure.
A collection of all the information
Here we have a collection of all the information you may need about the Prime Factors of 16. We will give you the definition of Prime Factors of 16, show you how to find the Prime Factors of 16 (Prime Factorization of 16) by creating a Prime Factor Tree of 16, tell you how many Prime Factors of 16 there are, and we will show you the Product of Prime Factors of 16.
Find the Factors is a type of logic puzzle. To solve one of the above puzzles, place the numbers 1 – 10 in both the top row and in the first column so that those numbers are factors of the given clues. For each puzzle, there is only one solution. Click on 10 Factors 2013-12-16 to find these and a few more puzzles, as well as last Monday’s solutions.
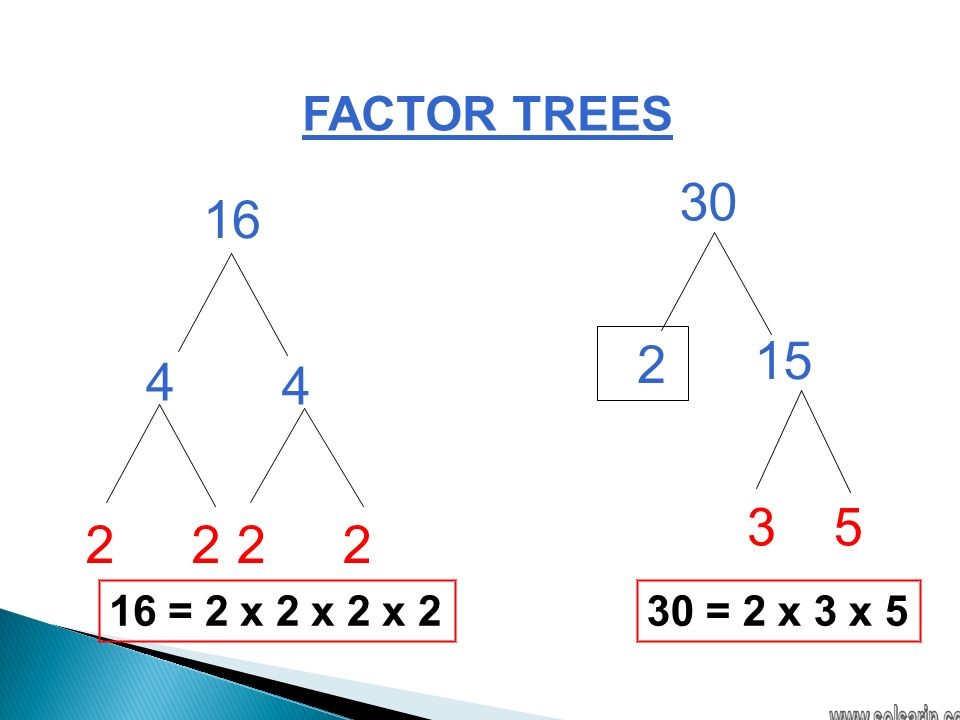

16 is a composite number, and it is 4 squared. 16 = 1 x 16, 2 x 8, or 4 x 4. Factors of 16: 1, 2, 4, 8, 16. Prime factorization: 16 = 2 x 2 x 2 x 2, which can also be written 16 = 2⁴.
Since √16 = 4, a whole number, 16 is a perfect square.
When 16 is a clue in the FIND THE FACTORS puzzles, use either 2 x 8 or 4 x 4. Only one of those sets of factors will work for any particular puzzle.
What are the Factors of 16?
The factors of 16 are the numbers that divide the number 16 completely without leaving any remainder. As the number 16 is a composite number, it has more than one factor. The factors of 16 are 1, 2, 4, 8 and 16. Similarly, the negative factors of 16 are -1, -2, -4, -8 and -16.
How to calculate the Factors of 16?
Go through the following steps to calculate the factors of 16.
- First, write the number 16.
- Find the two numbers, which gives the result as 16 under the multiplication, say 2 and 8, such as 2 × 8 = 16.
- We know that 2 is a prime number that has only two factors, i.e., 1 and the number itself (1 and 2). So, it cannot be further factorized.
- Look at the number 8, which is a composite number but not a prime number. So it can be further factorized.
- 8 can be factored as 2 x 2 x 2 x 1.
- Therefore, the factorization of 16 is written as, 16 = 2 × 2 × 2 × 2 x 1.
Prime Factors of 16 By Division Method
The number 16 is a composite and it must have prime factors. Now let us know how to calculate the prime factors of 16.
-
- The first step is to divide the number 16 with the smallest prime number, say 2.
- 16 ÷ 2 = 8
-
- Again divide 8 by 2 and the process goes on.
- 8 ÷ 2 = 4
- 4 ÷ 2 = 2
- 2 ÷ 2 = 1
Finally, we received the number 1 at the end of the division process. So that we cannot proceed further. So, the prime factors of 16 are written as 2 × 2 × 2 x 2 or 24, where 2 is a prime number.
Examples
Example 1:
Find the common factor of 16 and 15.
Solution:
The factors of 16 are 1, 2, 4, 8 and 16.
The factors of 15 are 1, 3, 5 and 15.
The common factor of 15 and 16 is 1.
Example 2:
What is the sum of factors of 16?
Solution:
We know that the factors of 16 are 1, 2, 4, 8 and 16.
Hence, the sum of factors of 16 is 1+2+4+8+16.
Sum of factors of 16 = 31
Example 3:
Find the common factors of 16 and 14.
Solution:
Factors of 16: 1, 2, 4, 8 and 16
Factors of 14: 1, 2, 7 and 14.
Hence, the common factors of 14 and 16 are 1 and 2.
- Factors of 16: 1, 2, 4, 8 and 16
- Negative Factors of 16: -1, -2, -4, -8 and -16
- Prime Factors of 16: 2
- Prime Factorization of 16: 2 × 2 × 2 × 2 = 24
- Sum of Factors of 16: 31
Factors of 16 by Division Method
- For finding the factors of 16 by division method, we will divide 16 by counting numbers and see which numbers exactly divide 16 and give 0 as a remainder.
- For example, when we divide 16 by 2 or 4 or 8, the remainder will be 0.
- At the same time, when we divide 16 by numbers like 3 or 5 or 7, it leaves a remainder.
- Let us divide and check for all numbers.
Thus, all numbers which leave a remainder 0 are the factors of 16. We see that 1, 2, 4, 8, and 16 are the factors of 16.
Explore factors using illustrations and interactive examples:
- Factors of 162- The factors of 162 are 1, 2, 3, 6, 9, 18, 27, 54, 81, and 162.
- Factors of 169- The factors of 169 are 1, 13, and 169.
- Factors of 216- The factors of 216 are 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 27, 36, 54, 72, 108, and 216.
- Factors of 160- The factors of 160 are 1, 2, 4, 5, 8, 10, 16, 20, 32, 40, 80 and 160.
- Factors of 168 – The factors of 168 are 1, 2, 3, 4, 6, 7, 8, 12, 14, 21, 24, 28, 42, 56, 84, and 168.
Factors of 16 by Prime Factorization
This is done by dividing 16 by prime numbers. We will then check if it does not leave any remainder and continue division with the quotient if it is a composite number. We can find the prime factors of 16 by the division method or the factor tree method.
Prime Factorization of 16 by the Factor Tree Method
Here we are finding the prime factors of 16, therefore, the root of our factor tree is 16. We write the pair of factors as the branch of 16.
2 is a prime number. Hence, the factor tree ends there. Hence, prime factorization of 16 is 2 × 2 × 2 × 2
Prime Factorization Of 16 By Upside Down Division Method
Here, 16 is an even number. So it is undoubtedly divisible by 2 with no remainder.Thus we do 16÷ 2 = 8.Now find the prime factors of the obtained quotient.Repeat Step 1 and Step 2 until we get a result of prime number as the quotient.Here, 8 is the quotient.8÷ 2 = 4. Here, 4 is the quotient.


How many Prime Factors of 16?
When we count the number of prime numbers above, we find that 16 has a total of 4 Prime Factors.
Factor Tree
Another way to do prime factorization is to use a factor tree. Below is a factor tree for the number 16.
A prime factor tree is a tree shaped diagram, where one finds the factors of a number, then the factors of those numbers, until one can’t factor any more. Note that each number on the left should be a prime number.
In number theory, the prime factors of a positive integer are the prime numbers that divide that integer exactly. The prime factorization of a positive integer is a list of the integer’s prime factors, together with their multiplicities; the process of determining these factors is called integer factorization. Type the number in the input box below to find the prime factors of that number.
Integer factors of 16 = 2, 4, 8, 16divided by 2, 2, 2, 2, gives no remainder. They are integers and prime numbers of 16, they are also called composite number.Prime number are numbers that can divide without remainder, This means that 16 is divisible by 2, 2, 2, 2, numbers
Thank you for staying with this post “prime factorization of 16” until the end.




